Estudo dos ângulos

Estudos dos ângulos, clique aqui!

Educação matemática I

Contextualizar a matemática é essencial para todos , se não, lamentavelmente continuamos a insistir que a inteligência e a racionalidade estão identificadas com matemática, continuando assim a papagaiar teoremas , decorar tabuada, mecanizar as operações e efetuar derivadas e integrais, que nada tem a ver com nada nas cidades, nos campos ou nas florestas.
Ubiratan D'Ambrózio - Doutor em matemática

Área do cŕculo

Classificação de triângulos

Educação Matemática

Para Elon Lages Lima*:

"Matemática não se aprende passivamente. Os exercícios ensinam a usar conceitos e proposições, desfazem certos mal-entendidos, ajudam a fixar na mente ideias novas, dão oportunidades para explorar as fronteiras da validez das teorias expostas no texto e reconhecer a necessidade das hipóteses, apresentam a aplicações de teoremas demonstrados e informam o leitor sobre resultados adicionais. [LIMA, Curso de Análise, vol. 1.]"
*Doutor, Univ. Chicago-1958
IMPA/RJ

O problema da caixa

Observe a caixa sem tampa e resolva.
Supõe-se que a caixa tenha as seguintes dimensões:
Largura: X
Comprimento: X+5
Altura: X - 10
Determine a área de papelão da caixa e o seu volume.
 Área: 5x² - 25x - 100 
 Volume: x³ - 5x² - 50x


Na animação abaixo, mova o ponto de corte dos cantos da caixa e observe que a medida que modificamos o corte, altera-se a altura da caixa, que representa seu volume, e a curva (parábola) que é criada, representa o tamanho do corte dos cantos da caixa.

Relações trigonométricas no triângulo retângulo

     Ramo da matemática, aplicada na medida de grandes distâncias, ou seja, aquelas que não conseguimos medir diretamente, utilizando instrumentos tradicionais de medidas. Serve a navegação, à agrimensura e à astronomia.
Ampliando-se seu estudo para a chamada trigonometria esférica, é usada na resolução de problemas da física, química e nas engenharias.

As razões trigonométricas
A palavra trigonometria vem do grego:
                                                       trigono: três ângulos
                                                            metria: medida
   Para entendermos estas razões, devemos entender os conceitos: cateto adjacente, cateto oposto e hipotenusa.
Essas definições estão relacionadas ao ângulo interno do triângulo retângulo que estamos estudando, com exceção da hipotenusa que sempre é o segmento (lado) de maior medida do referido triângulo.
   Pela imagem abaixo, se considerarmos o ângulo C, o lado oposto (cateto oposto) será o segmento AB (lado a). Neste caso, a razão chama-se seno do ângulo C (Sen C).
    Se considerarmos o ângulo agudo A, o lado oposto à este ângulo será o segmento BC (lado c). Visto isso, Seno de um ângulo é a razão entre o cateto oposto pela hipotenusa: cateto oposto / hipotenusa.

   Definimos assim o lado oposto ou cateto oposto.
   Por consequência, podemos definir o cateto ajacente, como sendo o outro cateto, logo o Cosseno (cos) de um ângulo é igual a razão do cateto adjacente pela hipotenusa.
   Para concluirmos, definimos a terceira razão trigonométrica, ou seja a razão igual ao cateto oposto pelo cateto adjacente, chama-se tangente (tg).
Logo temos algebricamente:

   Observe no vídeo, que referenciado-nos no ângulo (ζ) zeta, quando movemos o ponto correspondente, a abertura do ângulo modifica-se, consequentemente o valor de sua medida também, assim com relação às razões trigonométricas, verificamos que quando varia a abertura do ângulo, os valores das razões alteram-se também, conforme os conceitos relativos à seno, cosseno e tangente.

Adição algébrica

Adição algébrica de polinômios


Multiplicação de monômios


Multiplicação de polinômios
Para exemplificar a multiplicação de polinômios, vamos utilizar o modelo matemático do cálculo do volume de um sólido geométrico, no caso, o cálculo do volume de um paralelepípedo, conforme imagem abaixo:

Divisão de polinômios

Fatoração

Estudo do volume
Como calcular o volume de um bloco retangular?
É simples, basta multiplicarmos, seu comprimento, por sua largura e por sua altura, então V=c . l. h, não esquecendo que as unidades de medidas para o volume, devem ser pensadas em medidas cúbicas, ou seja,m³, cm³, etc.



Se o sólido for um cubo, devemos lembrar que este tem suas faces e arestas (a) iguais, portanto seu volume será dado por V = a³.

Teorema de Tales

"Quando  retas paralelas são cortadas por retas transversais, as medidas dos segmentos correspondentes determinados nas transversais são proporcionais."
Vejamos:
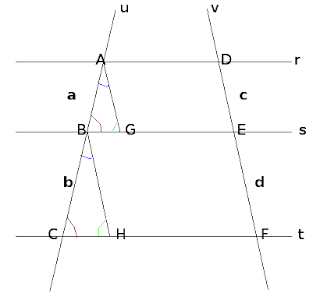
   Traçamos três retas paralelas r, s e t, cortadas por retas transversais u e v.

   Observe que os triângulos, são semelhantes pois, têm os ângulos correspondentes congruentes, logo as medidas dos lados correspondentes são proporcionais: (a construção dos triângulos, são usadas para provar a proporcionalidade dos segmentos formados pela interceptação das retas transversais pelas retas paralelas).

a/b = AG/BH

   Observamos também que: AG = c, pois são as medidas dos lados opostos do paralelogramo AGED.

                                           BH = d, pois são as medidas dos lados opostos do paralelogramo BHFE

Assim mostramos que há proporcionalidade entre eles:

a/b = c/d

    A partir do teorema de Tales podemos escrever outras proporções:

x/a = y/c

x/b = y/d

a/c = b/d

Teorema de Pitágoras

     Se construirmos quadrados sobre os lados a, b e c do triângulo retângulo, esses quadrados terão área a², b² e c².
     Assim podemos enunciar o Teorema de Pitágoras da seguinte forma: a área do quadrado construído sobre a hipotenusa é igual à soma das áreas dos dois quadrados construídos sobre os catetos.

Semelhança de triângulos

Teorema fundamental da semelhança de triângulos
     Toda reta que é paralela a um lado de um triângulo e intercepta os outros dois lados em dois pontos distintos determina com esses lados um segundo triângulo semelhante ao primeiro.

Equação do primeiro grau

     Ao resolvermos uma equação do primeiro grau, obtemos um resultado, esse resultado pode ser chamado de raiz da equação ou conjunto verdade ou conjunto solução da equação.
     Se substituirmos este resultado na incógnita, chegamos a uma igualdade numérica.
     Por exemplo:
     A expressão 2x - 10 = 4, é uma equação do 1º grau com uma incógnita (x). Resolvendo-a:

     2x - 10 = 4 -> 2x -10 +10 = 4 + 10 -> 2x = 14 -> 2x/2 = 14/2 -> x= 7, logo S=7.

     Portanto 7, é o conjunto verdade da equação, solução ou raiz da equação dada.

     Se substituirmos o x (incógnita) pela raiz, chegaremos a uma igualdade numérica, como a seguir:

     2 . 7 - 10 = 4 -> 14 - 10 = 4 -> 4 = 4, é uma igualdade numérica, logo tiramos a prova real de que 7 é a raiz da equação.

Cálculo das diagonais de um polígono

     Este cálculo pode ser efetuado pela fórmula: d= n(n-3)/2, onde d, representa o número de diagonais a serem descobertas e n representa do número de lados do polígono procurado.
Desvendando a fórmula
Por exemplo, dado um retângulo qualquer de vértices A,B, C e D.

     Isolamos um vértice, por exemplo, o vértice A. Para este vértice, somente é possível traçar uma diagonal com outro vértice não adjacente a ele.
     Criamos a fórmula: d= n-3, porque (-3)? Porque desconsideramos os outros 3 vértices em que não é possível traçar uma diagonal.
     A seguir aplicamos esta fórmula (d=n-3) ao retângulo em questão, então, como retângulo têm quatro lados (n=4), logo: d= 4 - 3, portanto para o vértice A, temos uma diagonal.
Ainda se temos uma fórmula que calcula o vértice do polígono, podemos então generalizar, isto é, para n lados, podemos multiplicar a fórmula obtida acima, para encontramos o número de diagonais de qualquer polígono.
     Mas observe que, uma diagonal tem dois sentidos (pois pode ser compartilhada por dois vértices), logo temos a necessidade de se dividir por dois, logo a fórmula é igual a:
                                                                 

Princípio fundamental da contagem

     Quando um evento é composto por n etapas sucessivas e independentes, de tal forma que as possibilidades   da primeira etapa é m e as possibilidades da segunda etapa é n, consideremos então que o número total de possibilidades de o evento ocorrer é dado pelo produto m.n.

Exemplo 1:

De quantos modos 3 pessoas podem sentar-se em 5 cadeiras em fila?
Logo: A primeira pessoa tem 5 opções;
          A segunda pessoa tem 4 opções;
          A terceira pessoa tem 3 opções, logo pelo princípio fundamental da contagem (PFC), temos:
          5 . 4 . 3 = 60, então as três pessoas tem 60 possibilidades.

Exemplo 2:

      Maria deseja formar um conjunto calça-blusa para vestir-se. Se ela dispõe de 4 calças e 6 blusas para escolher, de quantos modos pode forma o conjunto?