Teorema de Tales

"Quando  retas paralelas são cortadas por retas transversais, as medidas dos segmentos correspondentes determinados nas transversais são proporcionais."
Vejamos:
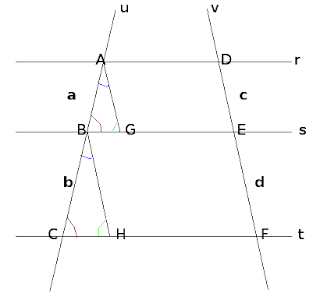
   Traçamos três retas paralelas r, s e t, cortadas por retas transversais u e v.

   Observe que os triângulos, são semelhantes pois, têm os ângulos correspondentes congruentes, logo as medidas dos lados correspondentes são proporcionais: (a construção dos triângulos, são usadas para provar a proporcionalidade dos segmentos formados pela interceptação das retas transversais pelas retas paralelas).

a/b = AG/BH

   Observamos também que: AG = c, pois são as medidas dos lados opostos do paralelogramo AGED.

                                           BH = d, pois são as medidas dos lados opostos do paralelogramo BHFE

Assim mostramos que há proporcionalidade entre eles:

a/b = c/d

    A partir do teorema de Tales podemos escrever outras proporções:

x/a = y/c

x/b = y/d

a/c = b/d